画中时空（二）

空间认知的相对性

大家可能在前面的内容中发现了一个特点，就是一旦观察者所处的视野基点发生改变，宇宙空间中用于辨别方位的上下左右全都不一样了。就像佛家的卍（万）字符，里面的笔划，这么看是横着的，那么看是竖着的；不过，即使转过来，当横着的笔划变成了竖着的，竖着的变成了横着的，卍还是卍。单从图象上看，卍字符本身各部位结构概念的相对性保证了图形的恒定不变。

可能有的朋友感受到了卍字符玄奥非凡，但又觉得对其内涵了解得不太清晰，是这样的。佛国世界、宇宙十方的很多不同层次的法理都只可意会而难以言述其点滴。这是人类的思维结构和语言的内在容量造成的，笔者这里也只能尽量以文字在最浅显的层面上简单表述一点基础的艺术理论。

苏轼在《题西林壁》里写道：“横看成岭侧成峰，远近高低各不同。”人们对于空间的认知，其实始终具有一种相对性。

这就好比站在南极的人所说的上方与站在北极的人说的上方完全相反。同样道理，哪怕是两人面对面，每个人的左手在对方看来都是右边那只手，而右手从对面看则是左边的手。

懂得这种相对性在绘画上是很重要的，大型绘画中最常见的天顶画就是建立在多视角构图基础上的一种艺术形式。对于一幅大型天顶画，如果进入可视范围的角度是开放的，站在东南西北各方向的观众自然都不希望自己看到的是一幅倒着的画。因此，艺术家在运用透视法构图时，就必须设身处地地为位于各个方向的观众考虑，尽可能从不同的视角思考如何建构出让每个位置的人都能看明白的作品。

图例：意大利画家科雷吉欧（Antonio da Correggio）为帕尔马主教座堂（Duomo di Parma）创作的天顶画《圣母升天图》（Assunzione della Vergine），作于1526年～1530年。

透视学就是建立在视觉空间相对性的基础之上的：当一个物体离人很近，哪怕一片小小的树叶在视野中都会显得很大；而当事物在远处时，即使一座山，也会相对显小。所谓“一叶障目，不见泰山”就是源于这种规律，在透视学中称之为“近大远小”，这也是透视学的基本原理之一。

不过，这些原理都有一个前提：它们只是在人类身处环境里的透视规律，一旦超出这个范围就不一定是这样了。比如早晨的太阳显得很大，而到了中午太阳则显得小，这就完全不符合透视学里近大远小的规律；再比如由于时空弯曲和光的运行状态等诸多原因，一些遥远的天体在天文望远镜里还会显示出类似近小远大的虚像状态。也就是说，人的理论只在人的层面内有效，而超出那个层次时，就是另一番天地了。

视野的远近大小不仅牵扯空间，甚至还与人对时间、速度等因素的感知相关。人的视觉机制有一个特点，就是在拥有广阔的视野时，远处快速移动的东西会显得较慢；而当人越靠近或者身临其境时，眼睛看到的运动则显得更快。举个例子，较慢的手枪子弹速度大约每秒钟三百米，但人眼完全跟不上这个速度；而运载火箭升空后的速度是用千米/秒来计算的，人眼却能轻松跟上比子弹快十几倍的火箭飞行速度，甚至还感觉火箭飞得挺慢。这里就有个不同参照空间范围内对时间感受相对性的问题。

不同范围的视野还能引发人在认知上的差异。比如以前有许多人认为在地上走直线只会越走越远，但通过卫星远离地面后拍摄照片，能看见地球是圆的。所以如果一直走直线，最后还是会绕一圈回到出发点。虽然生活中没几个人能感觉到脚下的地是圆的，但在辽阔的地面，直线其实是一种曲线。也就是说，当人身处某个局部的环境之中时，与整体的认知概念差异很大。

位相几何学（Topology）里有个经典结构叫莫比乌斯环（Möbius strip），用一根纸条旋转半圈后再把两端粘上就能做出来。我们假设有一个这样的环很长，长到一眼看不完全部，而只能看到局部，人们就会根据观察到的情况认为它有正反两个面；可是，当人了解到整体情况后就会发现：原来两个面都是一个面啊！在这里，“二”是“一”的局部，是不是很让人感慨？

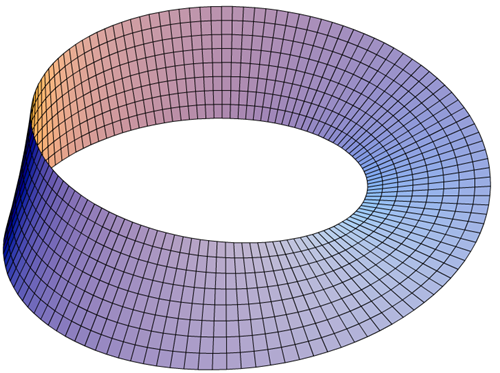图例：莫比乌斯环，是一种只有一个表面和一条边界的曲面。

当然，这里的“一”绝不是普通概念里的“一”。这个环是原本一个二维的平面经过扭曲后，出现在了三维空间中。假设一个只有二维概念的生物，顺着这个环不停地走，即使最后走完全程绕回原点，也只能对路径的结构做出种种猜测，诚可谓“只缘身在此山中”。

要想理解这“一个面”到底是怎么回事，必须具备三维的概念，立体地去看它的整体。就好比传统文化里讲的阴阳，本来就是一体，而并非大众习惯从局部认识的两个面。换句话说，只有站在更高层次，才能一眼看懂下面的层次；而在一个层次中要想弄清楚同一层次里所有的事情，就像庄子说的：“吾生也有涯，而知也无涯。以有涯随无涯，殆已。”

关于透视学与相对性的问题，对专业人士而言更为重要。美术专业的学生和工作者们在学校里都学过一些透视法，粗略地讲就是利用一些延伸到消失点（Vanishing point）的直线在画面中勾勒出立体形状的方法。据说青少年们在图画课上也会学一点这些基础内容，本文就此略过。

图例：常规透视法示意图，学校里教的透视法一般都是这样的。

图例：意大利画家皮萨内洛（Pisanello）所绘的透视图，25厘米 × 17.5厘米，作于十五世纪。

这里要谈的是，这种透视在人的视域中有一个极限。因为人眼对色彩和形状的感知集中在视野的中心，远离中心就会让看到的图象失真。目前的视觉理论将人的眼球静止不动时纵向视野的60度范围定为视野中心；由于人有左右两只眼睛，水平方向的角度要稍广一点。

也就是说，如果所观察对象的位置超出了视野中心，在透视上就会出现一个相应的扭曲，那么这时，学校里教的那些画直线的透视方法就不准了。这也就是为什么美术老师在教学生写生时，都要学生们与模特或静物保持一定距离。因为如果靠得太近，物像必然有大量超出视野中心的部份，就会造成画面的失真。

然而，在实际作画中，不可能把一切景象都控制在画家的视野中心，必然会有一部份出现在视野边缘，就像下面这幅照片一样。

图例：日本大阪市天王寺公园内一景。

一些细小的不同于经典透视学的部份暂且不谈，只看地面最靠近照片底部的几条横向地砖线条，仔细观察就能发现，它们其实是稍微呈圆弧状的。而如果根据常规的直线透视法，人们会把它们画成平行的直线。

这里就要引入一个比较少见的透视学术语，叫作曲线透视（Curvilinear perspective）。因为人的视网膜本身是半球形的，所以这种透视法更接近人眼看到的图象，尤其对超出视野中心物象的描绘，比直线透视更为准确。历史上不少画家都发现了这一点，也在他们的作品中做过相关尝试。

图例：法国画家富盖（Jean Fouquet）的小彩画《查理四世抵达圣德尼大教堂》（Arrival of Charles IV at the Basilica Saint-Denis），约作于1455年～1460年间。画家对前景的地板和其它一些地方采用了类似曲线透视的画法，只是略显夸张。

这些情况也体现了一个道理，就是即使在同一层次中，不同的学术理论也只能在一定的范围之内起作用，一旦超出这个范围，它们就不好使了。这时，就需要适用于不同范围的理论来代替或补充它，才不会被人为地禁锢在某些框架内无法突破。

关于绘画，还有一种相对而言的情况，就是虽然人们常把绘画归类为二维的艺术，但从技术角度看，它其实是三维的。具体说来，多数绘画都拥有某种“浅三维”的特质，它们除了有长度和宽度，还具备一个较浅的深度。而这里讲的深度并非单纯地指向颜料本身的厚度，而是色层间的差异所构造出的一种空间。

我们以一些常用的美术技法来举例，比如有的画家画人物，先把人画成裸体的，然后用半透明色给人罩上轻柔的衣衫，以此让服饰显得合身。这样，描绘服装的色料确实是画在了人物皮肤色料的外层，有一个前后的空间深度。由于颜料的透明度，观众也能同时看见内外的色层区别。

图例：意大利画家波提切利（Botticelli）的作品《春》（Primavera），203厘米 × 314厘米，木板坦培拉，约作于1478年～1482年间。作品描绘了神话时代里的几位神祇，画中几位女神身上透明的白色轻纱薄衣就是用透明和半透明色描绘在皮肤色层之上的。

另外，有些表现雾气、雨景的风景画也会采用类似画法。这些技巧能让画面展现出一种真实的内外深度，哪怕实际深度或许只有不到半个毫米。

还有一些画家，由于了解到这种浅三维在人的视觉中也能起作用，因此通过堆砌大量厚重的颜料，把一些油画、水粉之类的作品画成了浅浮雕。有人为了表现出立体感和空间感，在画头像时把鼻子等凸出的部位画得很厚，结果造成了画面严重开裂、颜料脱落，反而得不偿失。可见，对于艺术理论的运用，也必须与材料的性能结合起来，才能起到它该有的效果。

（待续）